Adapting clinical trials in health research: a guide for clinical researchers

Flexibility of design is not a panacea, but adaptive clinical trial designs offer the potential for more efficient research

Randomised controlled trials, when appropriately designed and conducted, can produce robust evidence for the safety and efficacy of health or medical interventions. In the traditional view, a trial is conducted according to a design that is “fixed” in that it follows criteria specified before the study's commencement, avoids amending design elements during the study, and analyses data only at the study's conclusion. Unless clearly documented or planned, mid‐study changes to the trial's design or interim looks at the data may undermine the validity of the trial's results.

In comparison, “adaptive” clinical trials allow pre‐specified changes to the trial's design or conduct during the study, without compromising the integrity of the trial. In an adaptive trial, the allowable changes and criteria for their adoption are specified in advance, with decisions based on results from interim analysis of the data accrued by that point. Changes may include stopping a trial early given evidence for treatment efficacy or futility, increasing the target sample size, adding or dropping treatment arms, or changing treatment arm allocation ratios.

Compared with a classical fixed design, an adaptive design can render a trial more efficient and/or ethical. For example, early stopping for futility reasons may reduce costs and unnecessary participant exposure to harm. However, the design, logistics and statistical analysis of an adaptive trial are more complex, and there may be situations where their potential benefits are outweighed by the disadvantages.

As biostatisticians, we find our colleagues’ willingness to consider an adaptive design can be hampered by factors including i) limited understanding of adaptive trial methodologies; ii) the increased complexity of designing and conducting an adaptive trial; iii) uncertainty about the adaptations applicable for a particular study; and iv) insufficient understanding regarding the relative benefits and disadvantages of an adaptive design, compared with the corresponding fixed design.

To further the understanding of adaptive designs among clinical researchers, we outline three elementary adaptations suitable for phase 2 or phase 3 trials. For each adaptation, we describe the type of research question it is suitable for, key design features, and potential benefits or disadvantages compared with the corresponding fixed design. We focus on three adaptations commonly used in practice: early stopping for efficacy or futility, sample size re‐estimation (SSR), and multi‐arm multistage (MAMS) studies, and discuss their characteristics within the familiar frequentist inferential framework (P values, confidence intervals, type I error, and power). More detailed reviews were published in 20201 and 2018.2

Early stopping for efficacy or futility: the group sequential design

Group sequential designs (GSDs) are one of the most widely used adaptive designs,3 allowing a trial to stop before recruiting the maximum sample size if interim data analyses provide clear evidence of either treatment efficacy or futility (Box 1). A GSD may be beneficial when there is uncertainty about whether a treatment is effective, or if a treatment effect is thought to potentially be larger than was assumed for the sample size calculation.

A GSD allows the maximum sample size to be accrued across two or more successive stages, with an interim analysis performed after each stage. The design pre‐specifies whether early stopping is allowed for efficacy, futility, or both, together with decision rules for early stopping or study continuation (Box 2). The maximum sample size per arm and typically, the number of interim analyses are also pre‐specified. If the efficacy or futility criterion is met after any interim analysis, the trial is stopped early; otherwise, participants are recruited for the next stage. If early stopping criteria are not met at any interim analysis, the trial recruits the maximum specified sample size to be used in the final analysis.

The key benefit of a GSD is a lower expected sample size than the corresponding fixed design due to the possibility of early stopping. However, because the expected sample size is a theoretical average over repeated executions of the same study, the sample size for a GSD allowing early stopping for efficacy may be slightly larger than for the fixed design if early stopping criteria are not met, due to the penalty associated with multiple hypothesis testing. Another disadvantage of the GSD is that early stopping may reduce the information available for important secondary outcomes or subgroup analyses.

Optimising power for efficacy testing: sample size re‐estimation

When designing a trial, there is often uncertainty about the value of parameters used to estimate the sample size. These parameters may include the baseline event rate for a binary response, the treatment effect size, or the variance of a continuous response. Estimates of these parameters are usually based on literature or pilot data, but such data may be unavailable or inaccurate. As a result, parameter values can be misspecified, resulting in a trial being under‐ or overpowered at the final analysis. The 2010 Consolidated Standards of Reporting Trials (CONSORT) guidelines noted a high prevalence of small trials with low power to detect clinically relevant effects in the published literature,4 suggesting a tendency for many trials to be underpowered.

SSR uses information from interim analyses to modify the target sample size if required, to ensure adequate power at the final analysis (Box 3). Although, theoretically, SSR can result in a sample size increase or decrease, in practice, only potential increases are considered.

Broadly, SSR methods are classified as blinded or unblinded. Blinded SSR uses interim data without revealing treatment assignments, to update the estimate of some parameter other than the treatment effect. Termed a “nuisance parameter”, this quantity is frequently the variance of a continuous response or the underlying event rate for a binary response. Blinded SSR methods are generally well accepted by governance and regulatory bodies and have minimal impact on type I error rates.5

In contrast, unblinded SSR requires revealing treatment assignments during the interim analysis, often to estimate the treatment effect itself. Unblinded SSR can be controversial, with care required to limit the parties having access to the treatment effect estimate and to maintain trial integrity. The risk of type I error inflation is also higher with unblinded SSR, necessitating non‐standard statistical tests.6

Some of these limitations of unblinded SSR are overcome by the “promising zone” method of Mehta and Pocock,7 which uses unblinded data to decide whether the conditional power — given the interim effect estimate and intended sample size — lies in a pre‐specified “promising zone”. If the conditional power lies in the promising zone (eg, 50–80%), the sample size is increased to achieve the target power; otherwise, the sample size is unchanged. An advantage of this method is its simplicity, with a standard final analysis being sufficient to protect the type I error rate.

Overall, SSR methods are quite straightforward to adopt and require relatively little planning at the design stage. When the treatment effect size is highly uncertain, an unexpectedly large effect can also be allowed for by combining SSR with a group sequential design, allowing early stopping for efficacy.8 The main disadvantage of SSR is some additional time required for the interim analysis.

Selecting the best treatment and dose: multi‐arm multistage studies

A common objective of phase 2 research is to identify the most effective treatment or dose from among multiple candidates. Using traditional fixed designs, separate two‐arm phase 2 studies might be performed to assess efficacy for multiple candidate treatments versus control, or a multi‐arm study could compare several treatments to a single control. Promising treatments could then be tested in subsequent phase 3 trials, each involving separate efforts towards design, conduct, governance and, often, funding.

Compared with conducting multiple, separate trials, an adaptive MAMS study can considerably increase efficiency.9 MAMS trials include various designs involving efficacy testing of multiple treatment arms using a shared control group, with different decisions allowable after one or more interim analyses; ineffective treatments may be dropped, the trial could be stopped early for efficacy or futility, or new treatment arms might be added. MAMS trials can be used for trialling an intervention at a single phase or can seamlessly combine phase 2 treatment selection and phase 3 efficacy testing in one study.

Benefits of the MAMS design include a more efficient use of available patients for testing multiple treatments; the flexibility to drop ineffective arms, add new arms or stop the trial early; and a shorter timeline for drug discovery. Disadvantages include the logistical complexity arising from not knowing which treatments will be continued and an inability to predict the final sample size.

A two‐stage “pick the winner” design is a modification of a MAMS study with somewhat less flexibility and correspondingly reduced complexity (Box 4). This design is conducted in just two stages, with a single experimental arm retained after a single interim analysis. Pre‐specifying the maximum sample size per arm and the timing of the interim analysis means the sample size is fixed, simplifying logistics and planning. A disadvantage is that if multiple treatment arms are effective, the design may not select the most effective arm for continuation.

Broad considerations for adaptive designs

Several broad considerations apply across adaptive designs. For an adaptive design to increase efficiency over a fixed design, outcomes need to be measured quickly, relative to participant accrual. Prompt data entry and a high standard of data management are also required throughout the trial to enable efficient, informative interim analyses. Statistical issues are also generally more complex, and a statistician is often involved throughout the entire study.

This brief review has described three simple, common adaptative designs suitable for phase 2 or phase 3 studies. Numerous other adaptations exist, for example, enabling changes to treatment allocation ratios (response adaptive randomisation) or biomarker‐defined patient populations (population enrichment). More complex master protocols, such as “basket” or “umbrella” designs, enable testing of a single treatment in multiple patient populations, or multiple treatments in a single population. Across designs, frequentist and Bayesian statistical approaches exist, offering distinct benefits and challenges. Bayesian methods are well suited to adaptive trials, by providing formal methods for combining prior information about a treatment effect with data accrued during a trial.

Conclusions

Adaptive designs encompass diverse methods and can improve the efficiency of randomised controlled trials. However, the design and conduct of an adaptive trial is more complex than for a traditional fixed design, with specific expertise and infrastructure often required. Flexibility of design is not a panacea, and the potential benefits and limitations of candidate designs require careful evaluation during trial planning. However, adaptive designs can offer the potential for more efficient research, and we believe many Australian researchers would welcome increased national capacity for their adoption.

Box 1 – Group sequential design (GSD) with two arms and three stages of equal size, with n patients collected at each stage*

---

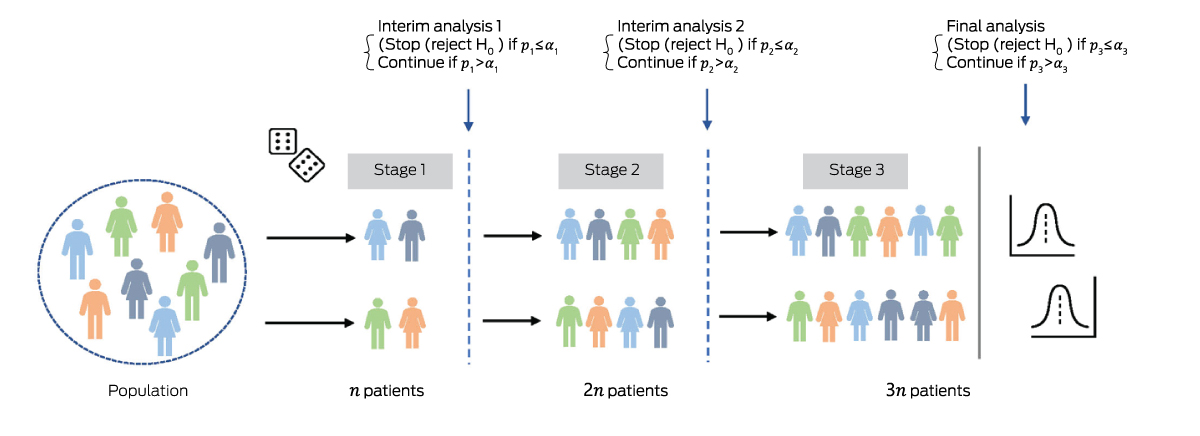
* There are two possible interim analyses, after which the trial either stops or continues to the next stage. If the trial does not stop early, the final analysis includes 3$n$ patients. A group sequential study can be designed to stop early for efficacy, futility, or both. The schematic shows a GSD allowing early stopping for efficacy only. After each stage, the null hypothesis is tested using all accumulated data. If the P value after stage $k$ is less than the pre‐specified significance threshold ($p_k\le {\alpha }_k)$), the trial stops early for efficacy; otherwise, it continues to the next stage. The ${\alpha }_k$ are defined to control the type I error rate at overall level $\alpha$ across all stages.

Box 2 – Stopping rules with discrete boundaries (left) and flexible α spending functions (right)*

---

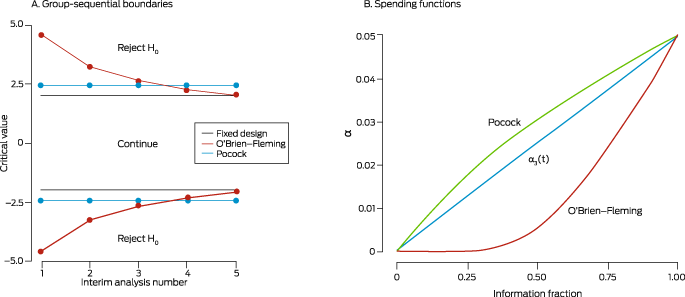
(A) Group sequential stopping boundaries for the Pocock (green line) and O'Brien‐Fleming (orange line) methods, for a planned trial with two treatment arms and five interim analyses planned to test efficacy only, conducted using equally sized stages. Interim analysis 5 coincides with the final analysis. At each interim analysis, a test statistic (eg, Z score) is computed using accumulated data and compared with the corresponding stopping boundary (critical value, corresponding to the α for that interim analysis). If the statistic does not exceed the boundary, the trial continues; otherwise, the null hypothesis is rejected, and the trial is stopped early for efficacy. Using Pocock stopping rules, the α (overall type I error) is spent at a constant rate, meaning stopping boundaries are equal across interim analyses. With O'Brien–Fleming rules, less α is spent early on, meaning stopping boundaries are high at earlier interims, and steadily decrease. Thus, with Pocock stopping rules there is a better chance of stopping the trial early. Conversely, with O'Brien–Fleming rules, the trial stops early only in the event of an unexpectedly larger effect, but there is a better chance of reaching the boundary at the end of the trial, due to spending less α at earlier analyses. The grey horizontal line depicts the corresponding fixed design, in which a final analysis is performed after all participants are recruited at α = 0.05 (corresponding to a test statistic critical value of ± 1.96). The Pocock stopping boundary at the end of the trial is much higher than for the fixed design, while the O'Brien–Fleming approach avoids this problem.(B) Continuous α spending functions are defined based on the information fraction (information available for the current sample, as a proportion of total expected information at the end of the trial; information is often related to the fraction of patients or observed events). The number of analyses need not be specified in advance, making these methods more flexible than using discrete boundaries. These functions start at zero (corresponding to the beginning of the trial) and increase to the nominal α (eg, 0.05) at the end of the trial. They are analogous to the idea of “spending” some of the total α at each interim analysis. The α spending functions corresponding to the discrete Pocock and O'Brien–Fleming stopping rules are shown, together with an arbitrary function ${\alpha }_3$(t).

Box 3 – Sample size re‐estimation for an adaptive trial with two arms and an initial final sample size of n₂*

---

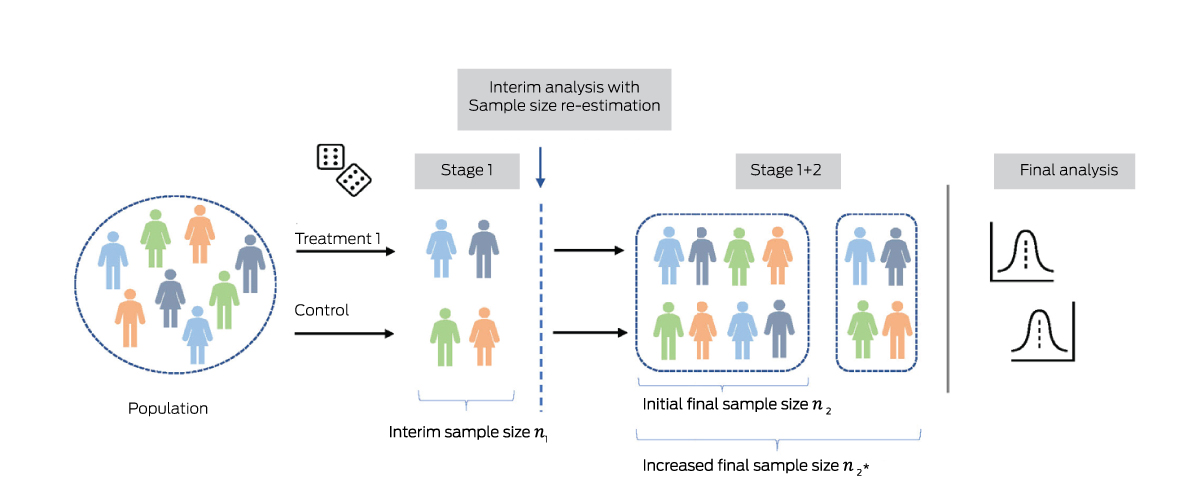
* After interim analysis using n₁ participants, the final sample size is increased from n₂ to $n_2^{*}$ to provide the desired conditional power (eg, 90%) at the final analysis, given the estimate of some parameter in interim data. This parameter may be the treatment effect itself, or another quantity influencing statistical power such as the variance of a continuous outcome, or the event proportion in controls (for a binary response).

Box 4 – Two‐stage “pick the winner” design, with two active treatment arms and a shared control arm*

---

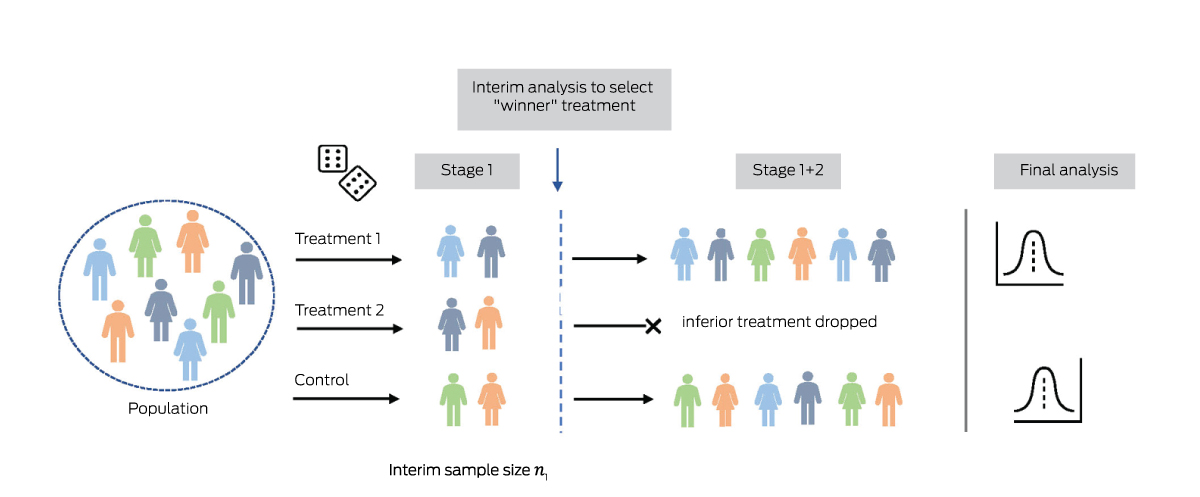
* In the interim analysis performed after the first stage, the most promising active treatment is selected. In the second stage, patients are randomised only to the identified “winner” treatment or the control arm.