Lifting lockdown when numbers are low but not zero means that superspreaders may remain, leading to a further wave of the epidemic
Superspreaders are a well known feature of some infectious diseases.1,2 Clearly, differing social roles will mean some infected people are more likely than others to spread a disease.3 For coronavirus disease 2019 (COVID‐19), biological factors are also important, as there may be a million‐fold variation in the viral load in secretions.4 Measurement of the number of secondary cases from a given primary case has shown that superspreading may be more important in COVID‐19 than in many other infections.5,6,7,8
To take an extreme example, if superspreaders were all important, so that the basic reproduction number (R0; the average number of cases expected to occur as a result of infection by a single individual in a fully susceptible population) of 2.5 was made up of 1% of infected people, who each spread the disease to 250 others and 99% who spread the disease to nobody, then there is at least a 99% chance that any randomly chosen infected person will not generate ongoing transmission. Even if, as would happen 1% of the time, the initial infected person was a superspreader, all the secondary cases generated may be in non‐spreaders, or even if a superspreader or two were included, the following generation of infected people may include no superspreaders, and so on. Fortunately, there is an area of mathematics — branching processes — that allows us to calculate algebraically the probability that the disease will eventually die out without chasing down the endless possible permutations.9,10
In reality, superspreading is not such an all‐or‐nothing phenomenon. Say we knew that 30% of infected people spread the disease to nobody, 50% spread it to just one person and the remaining 20% were superspreaders who spread the disease to 10 people. In this example, brief calculation shows that the average number of secondary cases generated by a randomly selected infected person is 2.5, and 20% of infected people account for 80% of the transmissions. This example is still artificial. Some infected people will transmit the disease to numbers other than 0, 1 or 10. A mathematical construct known as a negative binomial distribution with an average value, or R0, of 2.5 and an over‐dispersion parameter of 0.17 is able to provide a reasonable overall match to the available COVID‐19 data.5,6,7,8 (For simplicity here we use the notation R0 for this average value, although we note that the subscript “0”, strictly refers to the initial reproductive rate of the infection and it would be more precise to use “R” with subscripts “t” or “eff” to denote “R”, as it varies with time or the effectiveness of prevention measures.) This negative binomial distribution assigns various proportions of infected people to generate each possible number of secondary cases. This distribution is a little more extreme in terms of superspreaders than the previous example, in that 20% of cases account for about 90% of all transmissions. It can also be shown that just 5% of cases account for about half of all transmissions, and about 63% transmit the disease to no one (Box). Mathematical details are provided elsewhere.11
Here, we calculate the risk of disease re‐emergence using the scenarios of release from lockdown at a time when the lockdown has reduced the R0 to 0.8 and has been continued until a single symptomatic case remains; and release from lockdown one, or two, disease generations later. The calculations assume that there is no appreciable herd immunity and no quarantine‐free cross‐border human travel and, when lockdown is lifted, transmission immediately goes back to an average transmission rate of an R0 of 2.5. It is assumed that 50% of cases are asymptomatic and they are as infectious as the symptomatic cases.
We used the negative binomial distribution described above for the number of secondary COVID‐19 cases together with the theory of branching processes. If restrictions were lifted when there was just one case incubating the disease and the R0 returned to 2.5, then there is a 78% probability that there would not be any ongoing chain of cases. For each symptomatic case, however, there may be some asymptomatic cases. We assume that while the actual number of asymptomatics is random, the average number per symptomatic case is 1.0. If we take into account these asymptomatic cases, we can calculate algebraically that there is a 64% chance that the disease will die out once just a single case is recognised. To calculate the probabilities of disease re‐emergence when lockdown is extended, we used computer simulation. The probabilities that there will be no re‐emergence of disease if release from lockdown is delayed by one disease generation time or by two disease generation times are 96% and 99.6%, respectively.11
The simulation part of the model does not simulate cases on a day‐by‐day basis but in fixed units of non‐overlapping generations of the disease. These generations may be taken to represent a duration of a fortnight, which is the longest likely incubation period. A more sophisticated model would be calibrated in days and use overlapping generations, but this sophisticated modelling would be unlikely to substantially alter the results. However, a statement based on the current model that there is just “a single case” needs to be reinterpreted as “a single newly diagnosed case during the fortnight centred somewhere about the day of diagnosis”. While more sophisticated modelling would be desirable, the general conclusion that without reintroduction of cases from outside the region, the disease will likely be eliminated within a fortnight or so of no diagnosis of a new case would seem almost certainly valid.
Australia's initial COVID‐19 policy was to flatten the curve; that is, reduce the rate of exponential growth so that numbers rose slowly, giving us time to prepare and providing a lower peak that would be within the capacity of our intensive care unit bed numbers. The aim was to suppress the disease rather than eliminate it. Australia's lockdown proved to be more successful than anticipated and instead of slow exponential growth there was exponential decline with an R0 below 1.0. It brought the prospect of national elimination tantalisingly close. It is noteworthy that there are important but fine lines here. If lockdown had reduced our initial estimated R0 from 2.5 to only 1.5, we would still have had an unmanageably large epidemic and catastrophe. Even with an R0 of 1.2 that reduced the epidemic to a manageable level, there would still have been tens of thousands of deaths and a need to maintain some social restrictions for many more months or years. We did not flatten the curve, we stopped it. Although the disease was eliminated from some Australian states, lockdown was released just a little too soon. This, together with inadequate quarantine, allowed re‐emergence of the disease in Victoria and New South Wales.
The current suppression strategy in Australia is inadequate. The example of China shows that an elimination program can be retrieved from a far worse situation than exists currently in Australia. The examples of elimination in some Australian states and Pacific and East Asian nations also suggest that in the medium and longer term, an elimination strategy might be a lot cheaper than a lesser strategy of ongoing suppression. Our calculations show that if a lockdown resulted in a single remaining symptomatic case, given the relative rarity of superspreaders, disease elimination would be achieved far more rapidly than if there were just uniform exponential decay with an R0 of 0.8 (which would give an 80% chance that each infected person transmits the disease to another with each generation). Once elimination is achieved in Australia, maintaining elimination on an island continent with secure borders should be easier than it would be in many Western nations.
However, if lockdowns are lifted while some community transmission remains, there is the possibility that there could be a superspreader who passes the disease on to several other superspreaders and control will be lost. If effective measures are not continued for longer in Victoria and reintroduced in NSW, and border controls are relaxed too early, there is a risk of COVID‐19 catastrophe throughout Australia.
Of course, governments must factor in economic and ideological concerns along with epidemiological advice. The immediate economic cost of lockdown must be balanced against the economic risk of a second wave. The cost to individual freedom must be balanced against community protection. A world dichotomised into nations that have eliminated COVID‐19 and those that have not will be a world with severely restricted international travel. It will be a less globalised world, at least until an effective vaccine is available. Unfortunately, some of the epidemiological advice that government receives may already be diluted by such concerns, resulting in government decisions that underestimate the purely epidemiological issues.
Box – COVID‐19 transmission as a negative binomial function, illustrating the effect of superspreaders: cumulative proportion of secondary COVID‐19 infections attributable to primary cases of differing infectiousness
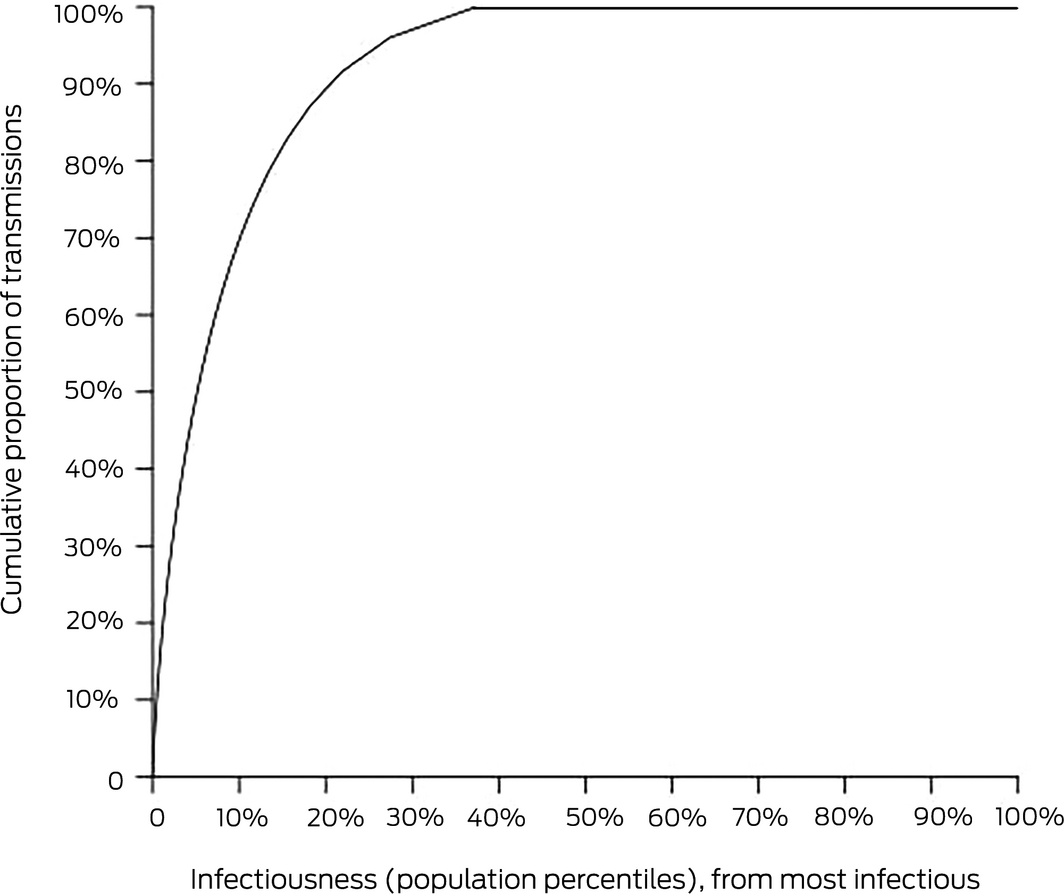
The horizontal axis is derived by ordering people from the most infectious to the least infectious and the distance along the axis shows the percentage of the population counted. The vertical axis shows the percentage of all transmissions that are accounted for by a given percentage of people on the horizontal axis. Because the least infectious 63% of the population actually transmit the disease to no one, the curve reaches 100% of transmissions at 37% on the horizontal axis.
Provenance: Not commissioned; externally peer reviewed.
- 1. Galvani A, May RM. Dimensions of superspreading. Nature 2005; 438: 293–295.
- 2. Lloyd‐Smith JO, Schreiber SJ, et al. Superspreading and the effect of individual variation on disease emergence. Nature 2005; 438: 355–359.
- 3. Zimmer C. Most people with coronavirus won't spread it. why do a few infect many? New York Times 2020; 30 June. https://www.nytimes.com/2020/06/30/science/how-coronavirus-spreads.html (viewed Aug 2020).
- 4. Gongalsky M. Early detection of superspreaders by mass group pool testing can mitigate COVID‐19 pandemic [preprint]. MedRXiv 2020; https://doi.org/10.1101/2020.04.22.20076166.
- 5. Endo A, Abbott S, Kucharski AJ, Funk S. Estimating the overdispersion in COVID‐19 transmission using outbreak sizes outside China [preprint]. Wellcome Open Res 2020; https://wellcomeopenresearch.org/articles/5-67.
- 6. Kucharski AJ, Russell TW, Diamond C, et al. Early dynamics of transmission and control of COVID‐19: a mathematical modelling study. Lancet Infect Dis 2020; 20: 553–558.
- 7. Qifang Bi, Yongshen Wu, Mei Shujiang, et al. Epidemiology and transmission of COVID‐19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study. Lancet Infect Dis 2020; 20: P911–P919.
- 8. Lau MSY, Grenfell B, Nelson K, Lopman B. Characterizing super‐spreading events and age‐specific infectivity of COVID‐19 transmission in Georgia, USA [preprint]. MedRXiv 2020; https://doi.org/10.1101/2020.06.20.20130476.
- 9. Feller W. Probability theory and its applications. Vol 1. 2nd ed. Wiley, 1961.
- 10. Kimmel M, Axelrod D. Branching processes in biology: interdisciplinary applied mathematics. Vol. 19. Springer, 2001.
- 11. Kault D. Superspreaders help covid‐19 elimination [preprint]. MedRXiv 2020; https://doi.org/10.1101/2020.04.19.20071761.





No relevant disclosures.